Estimating the Density Ratio between Distributions with High Discrepancy using Multinomial Logistic Regression
Abstract
|
Functions of the ratio of the densities p/q are widely used in machine learning to quantify the discrepancy between the two distributions p and q. For high-dimensional distributions, binary classification-based density ratio estimators have shown great promise. However, when densities are well separated, estimating the density ratio with a binary classifier is challenging. In this work, we show that the state-of-the-art density ratio estimators do perform poorly on well separated cases and demonstrate that this is due to distribution shifts between training and evaluation time. We present an alternative method that leverages multi-class classification for density ratio estimation and does not suffer from distribution shift issues. The method uses a set of auxiliary densities \{m_k\}_{k=1}^K and trains a multi-class logistic regression to classify the samples from p, q and {m_k\}_{k=1}^K into K+2 classes. We show that if these auxiliary densities are constructed such that they overlap with p and q, then a multi-class logistic regression
allows for estimating log p/q on the domain of any of the K+2 distributions and resolves the distribution shift problems of the current state-of-the-art methods.
We compare our method to state-of-the-art density ratio estimators on both synthetic and real datasets and demonstrate its superior performance on the tasks of density ratio estimation, mutual information estimation, and representation learning.
|
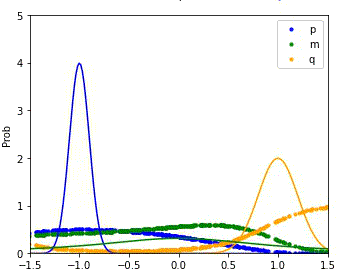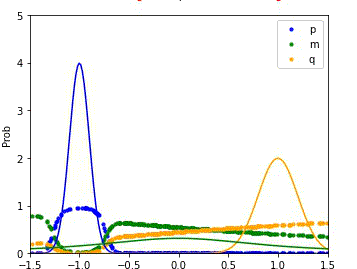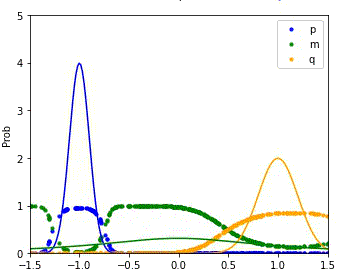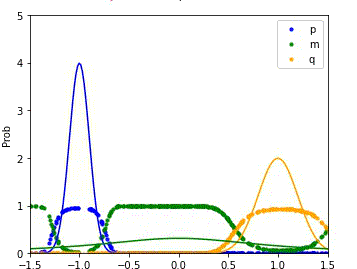
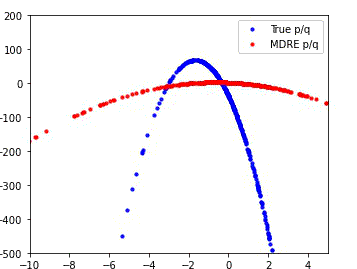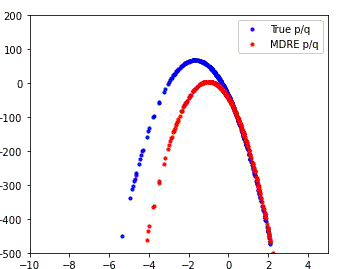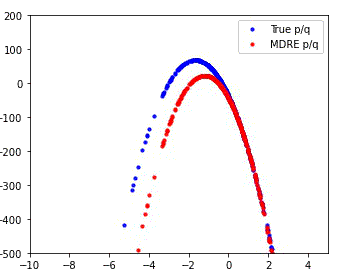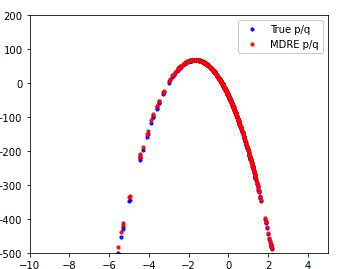
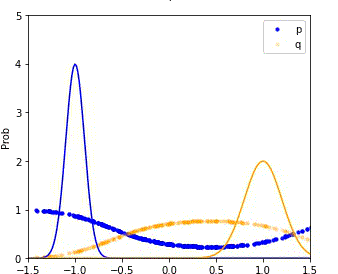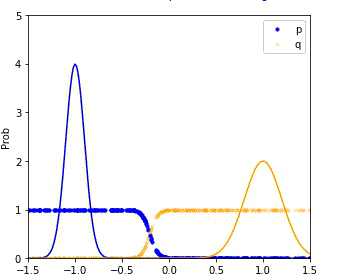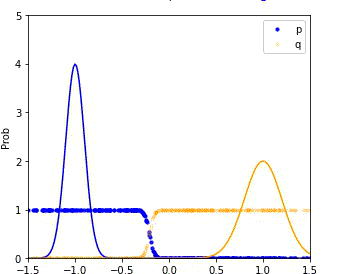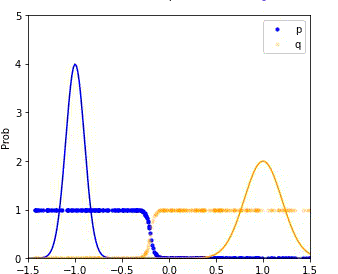
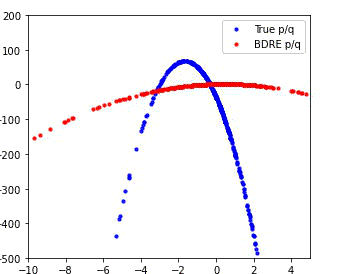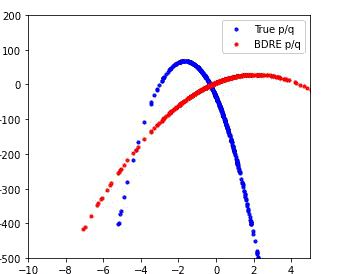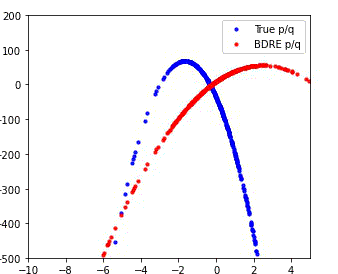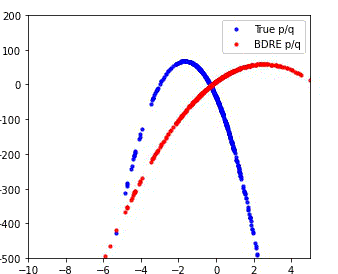
MDRE significantly better estimates the density ratio and is well-calibrated
We compare the performance of our method (MDRE) to the state-of-the-art density ratio estimator (BDRE) on a synthetic 1D dataset.
The first and third plots illustrate the learned decision boundaries for each of the distributions (p, q, m) and it is clear that MDRE is much better calibrated.
The second and fourth plots compare the ground truth and estimated density ratios and, once again, MDRE accurately learns the density ratio, whereas BDRE fails to do so.
MDRE estimates mutual information accurately even in high-dimensional settings
| Dim |
μ1 |
μ2 |
True MI |
BDRE |
TRE |
F-DRE |
MDRE (ours) |
| 40 |
0 |
0 |
20 |
10.90 ± 0.04 |
14.52 ± 2.07 |
14.87 ± 0.33 |
18.81 ± 0.15 |
| 40 |
-1 |
1 |
100 |
29.03 ± 0.09 |
33.95 ± 0.14 |
13.86 ± 0.26 |
119.96 ± 0.94 |
| 160 |
0 |
0 |
40 |
21.47 ± 2.62 |
34.09 ± 0.21 |
12.89 ± 0.87 |
38.71± 0.73 |
| 160 |
-0.5 |
0.6 |
136 |
24.88 ± 8.93 |
69.27 ± 0.24 |
13.74 ± 0.13 |
133.64 ± 3.70 |
| 320 |
0 |
0 |
80 |
23.47 ± 9.64 |
72.85 ± 3.93 |
9.17 ± 0.60 |
87.76 ± 0.77 |
| 320 |
-0.5 |
0.5 |
240 |
24.86 ± 4.07 |
100.18 ± 0.29 |
10.63 ± 0.03 |
217.14 ± 6.02 |
We compare the performance of MDRE along with other state-of-the-art density ratio estimators (BDRE, TRE, and F-DRE) on more complex, high-dimensional settings.
In all of the tasks, MDRE outperforms all other models in most accurately estimating the ground truth mutual information (MI).
MDRE learns better representations for classification
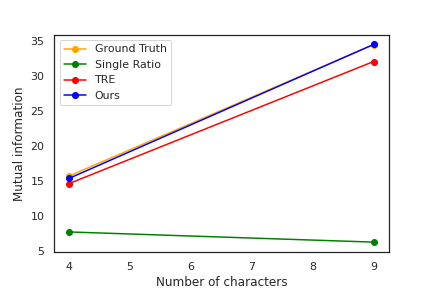
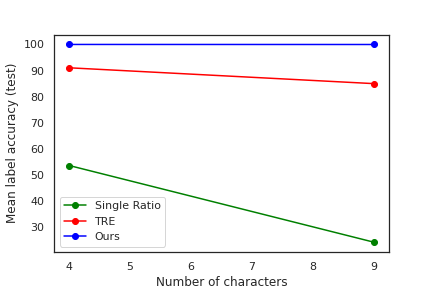
We also study our model in the context of a real-world task of mutual information estimation and representation learning with SpatialMultiOmniglot.
The leftmost figure illustrates that MDRE estimates the MI most accurately, and, therefore, our model achieves almost perfect classification accuracy.
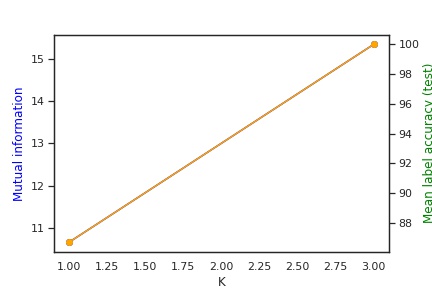
In the rightmost figure, we conduct an ablation study with varying sizes of K to show that the number of auxiliary distributions can significantly influence both MI estimation and classification performance.